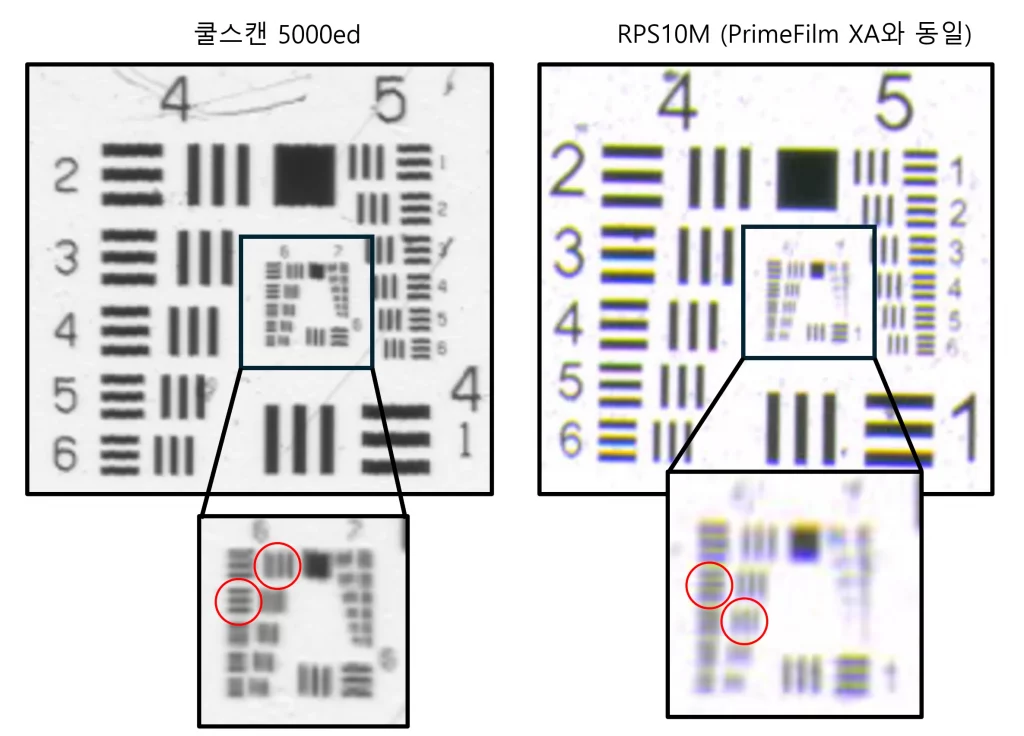
카메라로 슬라이드 필름을 스캔하려다 보면은 사진이 칼리브레이션이 제대로 되어있나 확인하고 싶을 수 있다. 필름 스캔은 다른 사진과 다르게 반사식 컬러차트가 아니라, 투과형 (필름식) 컬러차트를 사용해야 한다. 대부분의 스캐너 프로그램은 투과형 컬러차트 칼리브레이션이 내장되어 있으나, 카메라로 사진을 찍을 경우, 칼리브레이션이 간단하지는 않은데, 아래 포럼에서 설명을 잘 해주었길 래, 직접 해보고 한글로 사용기를 남겨본다.
https://forums.negativelabpro.com/t/color-management-custom-profiles-at-capture-slides/5161/11
1. 일단 슬라이드 필름을 찍는다.
ISO, F값, 셔터속도 등등 모든 상황을 동일하게 유지한체, IT8과 찍고 싶은 슬라이드를 전부 찍어준다. 참고로 로우 사진을 저장해야 된다.

2. DCRaw를 이용해서 사진을 TIFF로 변환하자.
일단 DCRaw를 받자.
https://github.com/ncruces/dcraw/releases/tag/v9.28.8-win
여기서 dcraw-windows.zip을 눌러서 다운 받자.
DCraw는 커맨드라인 프로그램이기 때문에 터미널에서 실행을 시켜야 한다. 편의를 위해서 폴더 안에 pictures라는 폴더를 만들어 놓고 찍은 로우사진을 전부 옮겨주자.
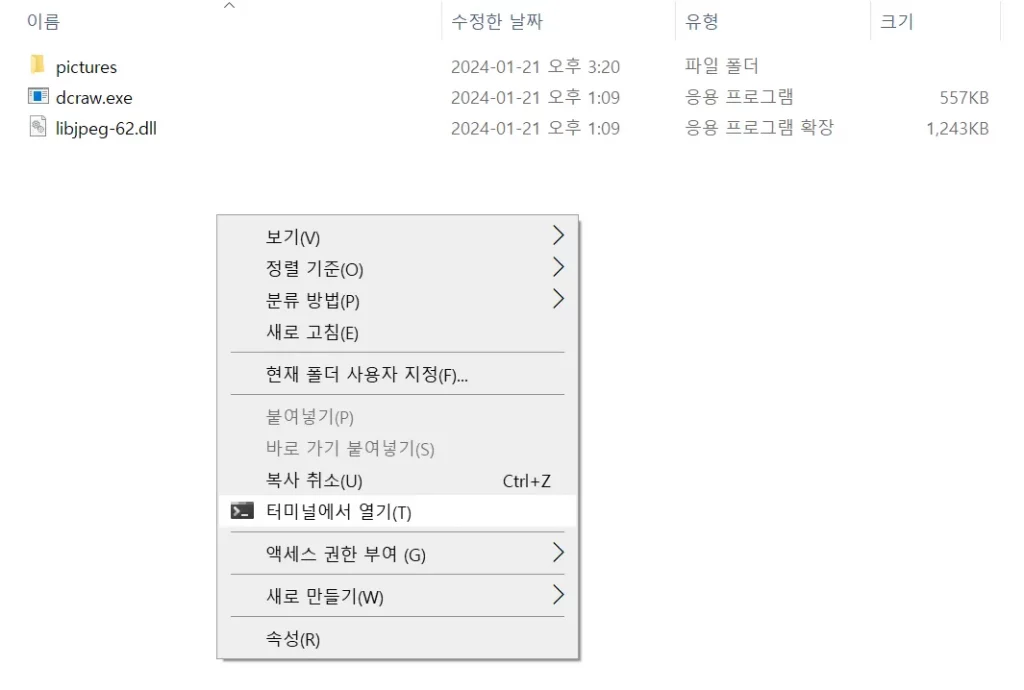
그 다음 폴더에서 오른쪽 클릭을 한 뒤, 터미널에서 열기를 눌러주자.
그리고 터미널에 다음과 같이 입력을 한 뒤, 엔터를 눌러주자. (파일 이름은 알맞게 교체)
.\dcraw.exe -v -T -o 5 -j -M -6 -W -g 1 1 -w .\pictures\DSC04722.ARW .\pictures\DSC04723.ARW .\pictures\DSC04724.ARW .\pictures\DSC04725.ARW .\pictures\DSC04726.ARW .\pictures\DSC04727.ARW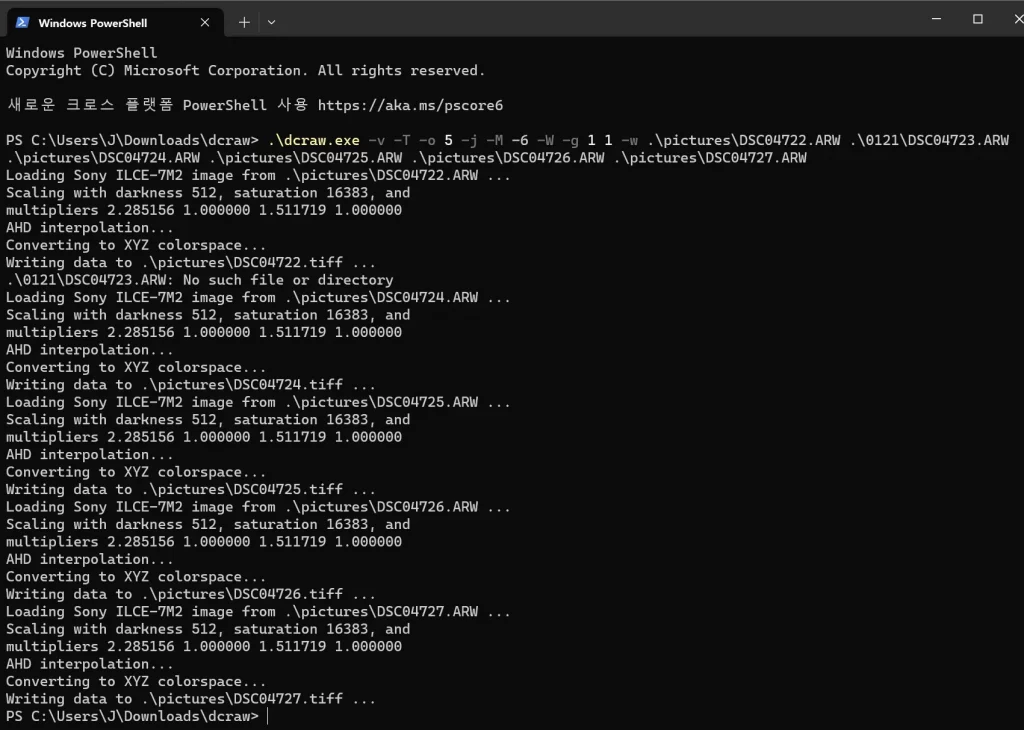
그럼 모든 사진을 TIFF로 바꿔준다. 참고로 감마 값을 선형으로 바꾸었기 때문에, 어둡게 변환된 것을 확인 할 수 있다.

3. Argyll Color Management System 다운로드 및 Scanin으로 차트 인식
https://www.argyllcms.com/에 들어가서 맨 밑에
Download V3.1.0 Main Microsoft Windows executables를 누르고 X86 64 Bit를 눌러 64비트 프로그램을 받아주자. 나는 usb\ArgyllCMS_install_USB.exe를 눌러서 설치를 했는 데, 지금 보니까 우리가 사용할 프로그램은 굳이 설치가 필요 없는 것 같다.
이제 Scanin으로 IT8 사진을 인식을 해야하는 데, 가끔씩 뻑날 수가 있으니까 포토샵으로 크롭을 해주자.
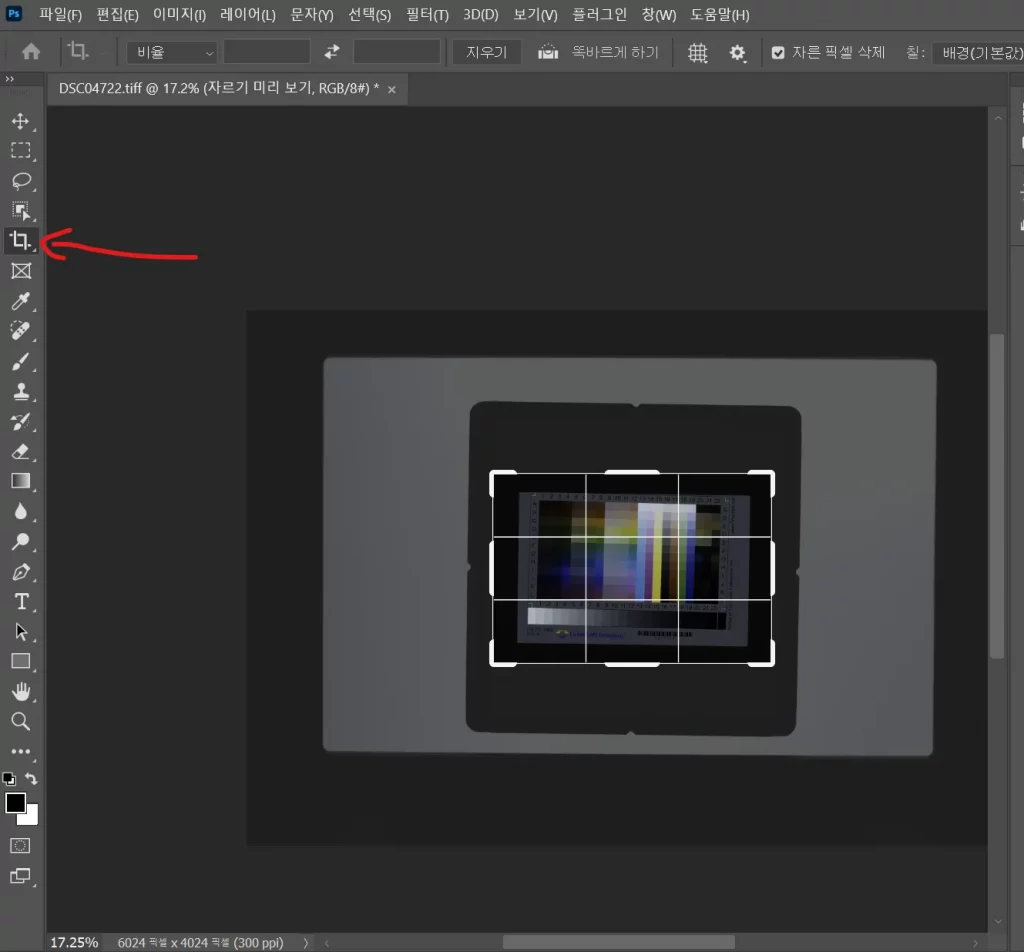
왼쪽의 자르기 도구를 사용해서 적당히 잘라주고, Ctrl+S를 하면, 내보내기 할 필요 없이 알아서 원본 TIFF에 바로 덮어쓰기가 된다.
편의를 위해서 Argyll폴더에 있던 it8Wolf.cht와 IT8을 구매하면서 같이 다운로드 받은 IT8 Batch Measurement 파일을 dcraw로 옮겨주자.
이후 터미널에서 다음과 같이 쳐주자. scanin.exe의 위치는 알맞게 쳐주자.
..\Argyll_V3.1.0_win64_exe\Argyll_V3.1.0\bin\scanin.exe -v -dipoan -G 1.0 -p .\pictures\DSC04722.tiff .\it8Wolf.cht .\E210610.txt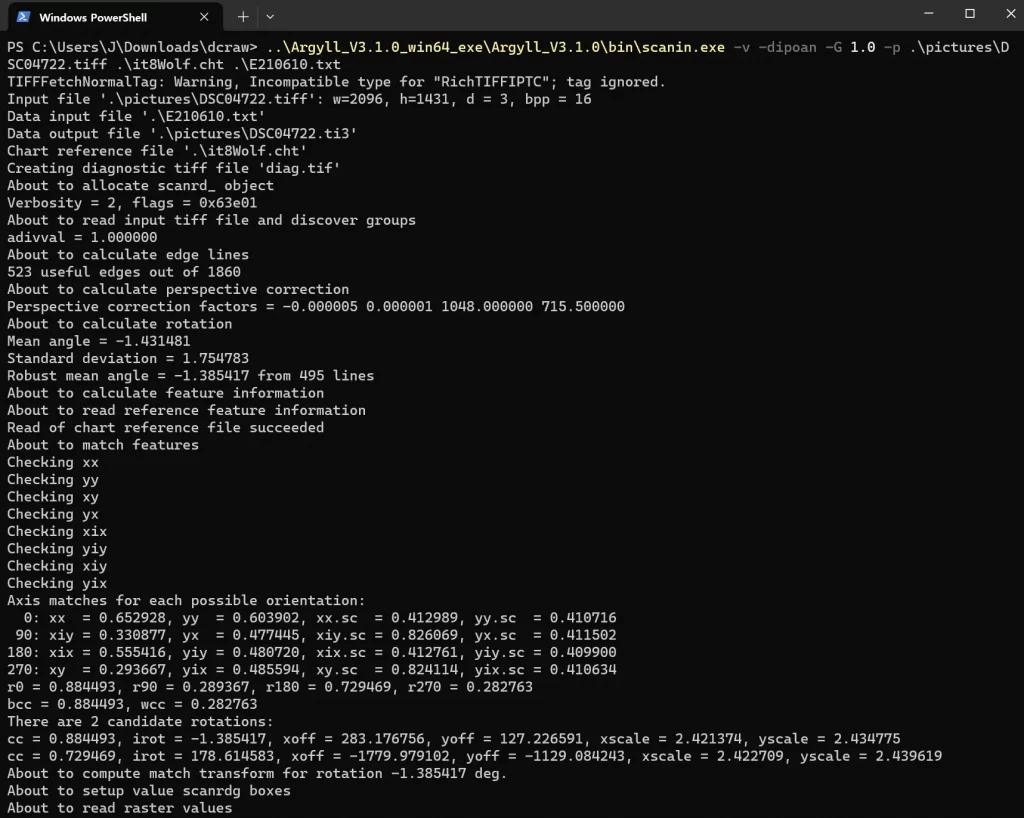
그럼 어쩌구 저쩌구 하면서 파일이 두 개가 만들어지는 데, 일단 diag.tiff를 확인해주자.

위와 같이 제대로 인식이 됬으면 성공한거고, 제대로 안되면 크롭하고 다시 돌려보자.
4. 프로파일 생성 및 결과 값 확인
다음과 같이 터미널에 입력하자. 보정 프로파일을 여러번 생성할 수도 있으니까 오늘 날짜를 이름으로 넣어서 프로필을 생성했다. 이거는 알아서 좋은 이름을 골라보자.
..\Argyll_V3.1.0_win64_exe\Argyll_V3.1.0\bin\colprof.exe -v -D"20230121" -qm -am -u .\pictures\DSC04722이러면 DSC04722.icm이라는 파일이 만들어 졌다. 이후, 제대로 됐는 지 확인하기 위해 profcheck.exe를 돌려 보자
..\Argyll_V3.1.0_win64_exe\Argyll_V3.1.0\bin\profcheck.exe -v2 -k .\pictures\DSC04722.ti3 .\pictures\DSC04722.icm결과 숫자과 다음과 같으면 괜찮다는 것 같다. 이 값이 정확히 어떤 의미인지는 사실 잘 모르겠다.
Profile check complete, errors(CIEDE2000): max. = 4.532432, avg. = 1.401173, RMS = 1.634565
5. 프로파일 할당
이건 포토샵으로도 되는데 Argyll로도 된다. 근데 이건 한줄로 여러파일은 안 되는거 같아서 여러줄을 한 번에 적어놓고 복붙하면 될듯 하다.
..\Argyll_V3.1.0_win64_exe\Argyll_V3.1.0\bin\cctiff.exe -e .\pictures\DSC04722.icm .\pictures\DSC04722.tiff .\pictures\DSC04722_conv.tiff
..\Argyll_V3.1.0_win64_exe\Argyll_V3.1.0\bin\cctiff.exe -e .\pictures\DSC04722.icm .\pictures\DSC04723.tiff .\pictures\DSC04723_conv.tiff
..\Argyll_V3.1.0_win64_exe\Argyll_V3.1.0\bin\cctiff.exe -e .\pictures\DSC04722.icm .\pictures\DSC04724.tiff .\pictures\DSC04724_conv.tiff
..\Argyll_V3.1.0_win64_exe\Argyll_V3.1.0\bin\cctiff.exe -e .\pictures\DSC04722.icm .\pictures\DSC04725.tiff .\pictures\DSC04725_conv.tiff
..\Argyll_V3.1.0_win64_exe\Argyll_V3.1.0\bin\cctiff.exe -e .\pictures\DSC04722.icm .\pictures\DSC04726.tiff .\pictures\DSC04726_conv.tiff
..\Argyll_V3.1.0_win64_exe\Argyll_V3.1.0\bin\cctiff.exe -e .\pictures\DSC04722.icm .\pictures\DSC04727.tiff .\pictures\DSC04727_conv.tiff