상이고 뭐고 엄청 많이 받았는데 솔직히 잘 모르겠다. 되게 잔잔하구나 라는 느낌을 받았는데, 감정의 절제가 어느정도 있어서, 미국 의료보험의 문제점도 담담하게 넘어가고, 경제 실패에 대한 이야기도 담담하게 넘어간다.

다만 나같은 문외한에게는 재미없는 영화였지만 이런걸 열심히 봐줘야 보는 눈이 생기는게 아닐까.

그래도 재미는 없어서
3/5

별로 재미 없음. 스토리가 빈약하고 액션이 메인인 영화인데, 요즘 보기에는 조금 촌스러움

2/5

기댓값(Expected Value)이란 확률과 그 사건에 대한 결과를 곱한 것의 합을 말한다.

예를 들어, 사탕 2개를 얻을 확률이 $latex \frac{1}{2}$, 사탕 3개를 얻을 확률이 $latex \frac{1}{2}$라면, 얻는 사탕의 기댓값은 2.5개가 된다.

만약 슈퍼맨이 인류를 모두 죽일 확률이 0.0001프로이고, 아무도 죽이지 않을 확률이 99.9999프로라면 기댓값은 어떻게 될까? 인류의 멸종은 꽤나 큰 피해이기 때문에, 사건에 대한 결과를 – ∞ 로 둔다면, 기대 값은 확률이 아무리 작아도 – ∞ 가 되게 된다.

세계 최고 감독 갓스나이더의 영화 돈옵저의 파이널 트레일러를 보면 다음과 같은 대사가 나온다.

He has the power to wipe out the entire human race. If we believe there is even a 1% chance that he is our enemy, we have to take it as an absolute certainty.

즉, 슈퍼맨이 인류의 적이 될 확률이 1프로만 된다고 해도, 이의 기댓값은 100프로의 확률과 동일하다는 의미다. 잭 스나이더 감독은 배트맨이 슈퍼맨과 적대하게 되는 이유를 그렇게 설명했지만, 잭 스나이더의 고질적인 스토리 설명의 문제 때문에 이 설명은 관객에게 제대로 이해시키지 못해서 결국 사람들은 “그래서 왜 싸우는 거냐?” 라는 궁금증을 끝까지 가지게 되었다.

제발 마블 스나이더 고용해서 액션 종신감독 시키면 안되냐?

1970년대에는 테두리 없는 사진이 유행했다면 1960년대에는 울퉁불퉁한 사진 테두리가 유행했었다. 패션처럼 사진에도 유행을 돌고도는데 그중 하나는 검은 테두리의 사진이다. 

검은 테두리는 흑백사진에서 하얀색 피사체와 배경을 분리해주는 역할이 있고, 사진 자체에 깊이를 주기때문에 많은 사람들이 선호하는 테두리이다. 

특히 검은색 테두리의 경우, 크로핑을 좋아하지 않는 여러 사진 작가들이 자주 쓰곤 했는데, 이는 사진을 필름에서 인화하는 도중 인화된 사진은 자연스럽게 주변에 검은 색 테두리가 생겼고, 이를 가위질 하지 않았다는 걸 보여주기 위해서, 그대로 출판을 하곤 했다. 물론 크로핑을 한 뒤 검은 색 테두리를 추가할수도 있긴 하다. 디지털 사진의 시대가 되어서도 이런 전통이 아직도 남아있어서, 크로핑 하지 않은 사진의 경우 검은 색 테두리를 넣기도 한다.

나는 내가 찍은 사진을 인스타그램에 올리는 데, 확실히 어느정도 테두리, 하얀 색 테두리를 넣었을 경우 사진이 이쁘게 나온다. 이는 인스타그램 페이지가 정사각형 사진에 최적화 되어있고, (초창기에는 정사각형 사진만 업로드 가능했음), 그렇기 때문에 다른 비율의 사진을 넣었을 경우 중앙만 보여주기 때문에 지저분해 보인다. 

• 

• 

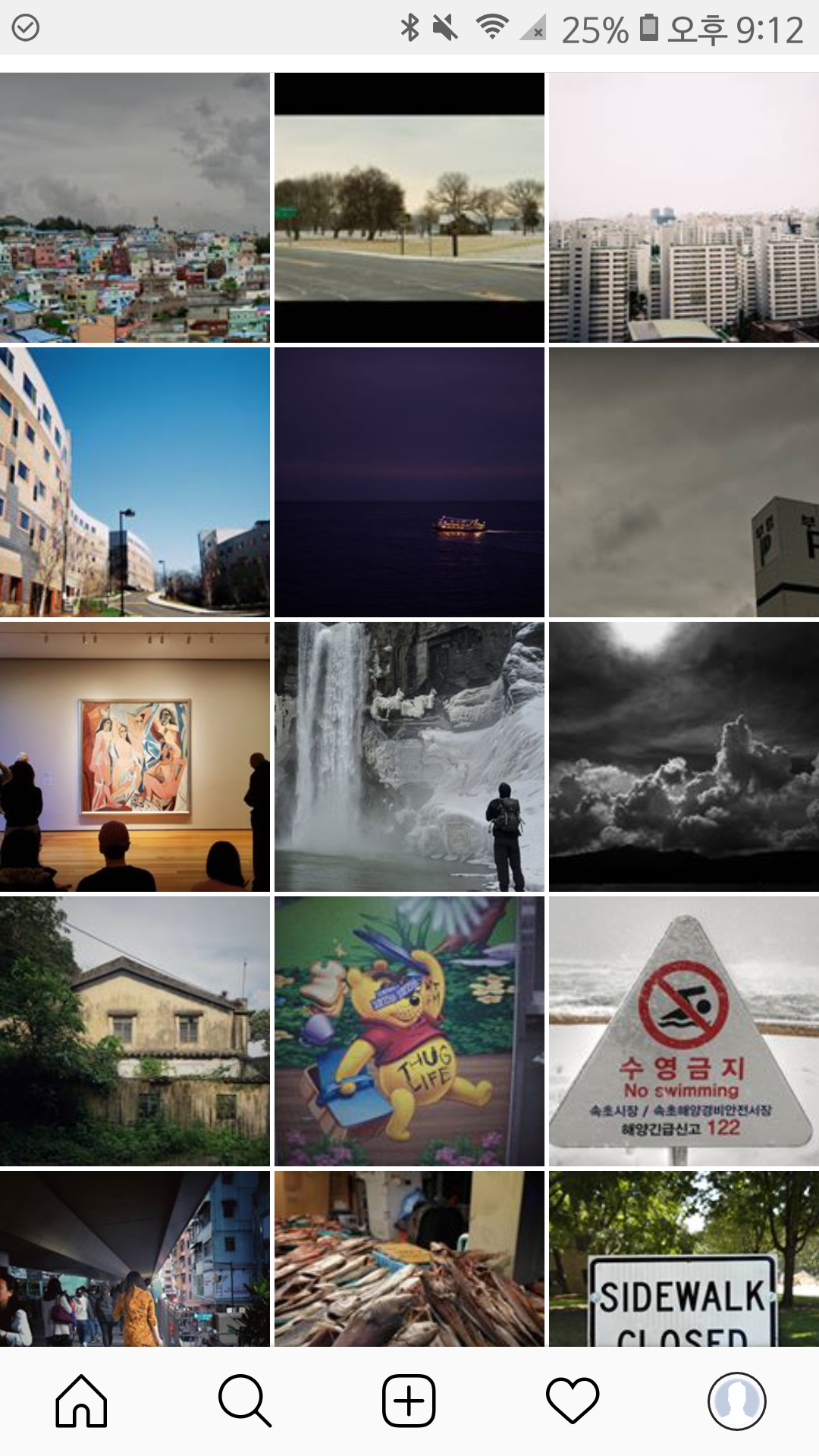
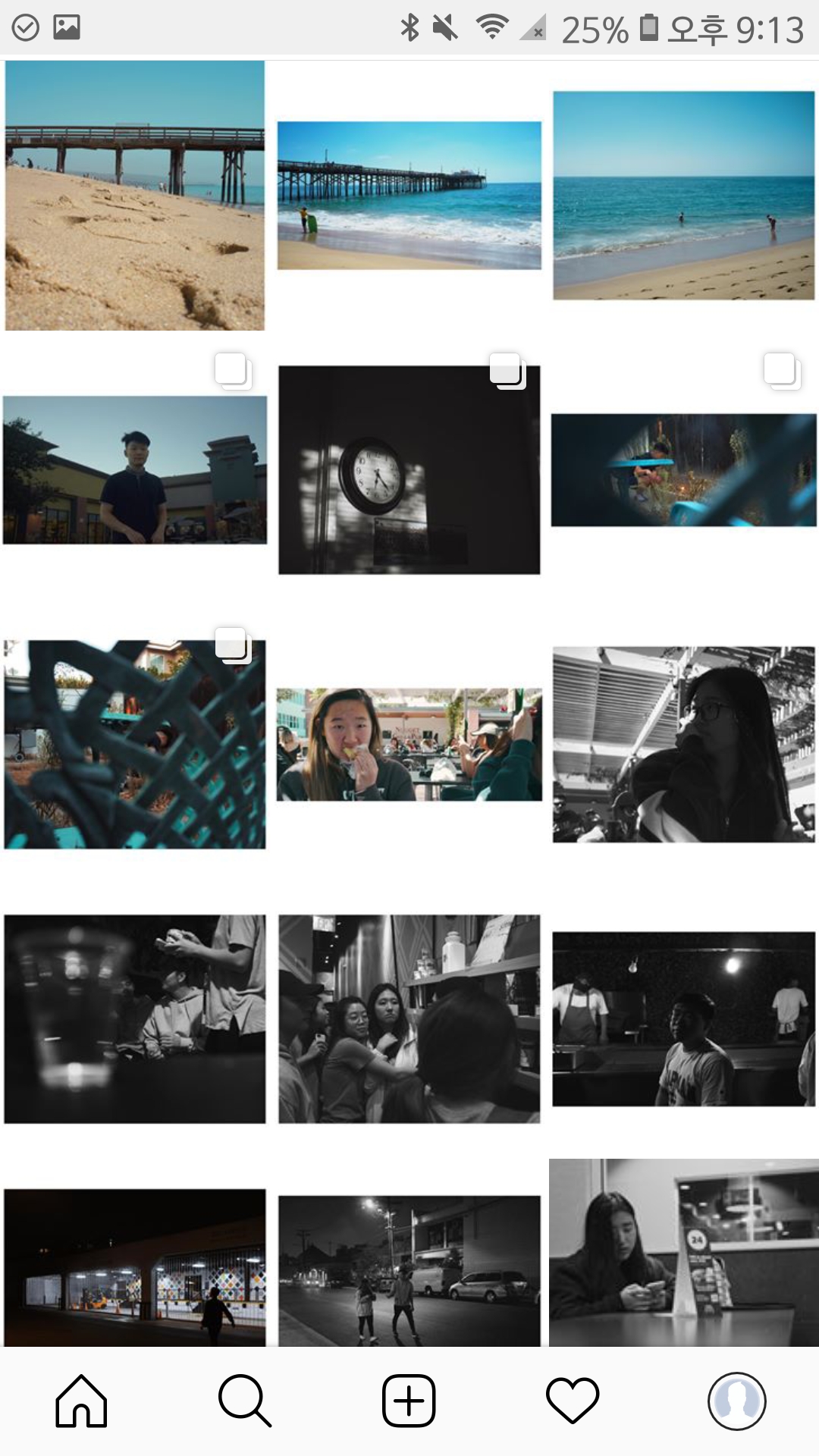
작가가 생각한 사진의 비율과 구도에 무관하게 정사각형으로 잘라서 보여주기 때문에 어떤 사람들은 사진을 넓혀서 정사각형으로 만든뒤 업로드 한다. 주로 사진은 가로가 더 넓기때문에 위에 여백을 좀더 두기만 하면 더 깔끔해 보인다. 
여기서 약간의 변형을 주면, 마치 갤러리에 사진을 붙혀 놓은 듯한 모습을 보여줄 수 도 있다.

나는 딱히 사진을 외부적으로 손을 대기가 싫어서, 구도를 위한 크로핑을 제외하고는 테두리를 따로 추가를 하지는 않는다. 만약 사진을 출판할 일이 있다면, 생각을 하겠지만, 지금은 사진을 그 자체로 생각을 하기 때문에 테두리를 선호하지는 않는다. 

그럼에도 불구하고 저번 사진중 하나는 깊게 테두리를 주었다. 특히 검은 색 테두리는 인스타그램과 어울리지 않는 데도 말이다. 이 사진은 위아래로 크로핑을 깊게 했기 때문에 맨 위에 서술한, 크로핑을 안했다는 이유로 테두리가 있는 것은 아니다. 

나는 예전부터 영화를 좋아했고, 영화에 대한 구도도 좋아했다. 사진과는 다르게 영화는 시간축에 대한 구도도 존재하는 영상작품이기에 사진보다 한 차원 더 높은 예술이라고 생각을 한다. 
언젠가 기회가 된다면 사진이 아닌 짧은 5초 짜리 영상도 올리고 싶은 마음이 있다. 

요즘 영화는 21:9의 구도로 나오고, 사람들은 4:3 화면에서 이를 소비한다. 요즘 티비나 컴퓨터 모니터는 기본이 4:3이기에 (1920: 1080), 영화를 볼때면 위 아래로 그 차이만큼의 검은 여백이 생기는데 이를 모방해서, 사진이지만 마치 영화의 한장면 같은 느낌을 주고 싶어서 넣어 보았다. 
그 외에 색감이나 그레인도 어느정도 추가해서 비슷한 느낌을 주어 봤는데 아무래도 영화는 망원렌즈를 주로 쓰기 때문에, 48mm 각도로는 비슷한 느낌을 주기 힘들지만서도, 어느정도 비슷한 느낌을 준거 같기도 하다. 기회가 된다면 짧은 영상들도 올려보고 싶다.

노인을 위한 나라는 없다 (2007) 을 감독한 코엔형제의 작품이다.

하나의 사건을 가지고 여러 인물이 꼬인다는 점이 최근에 본 여러 작품들과 비슷하다.

넷플릭스의 Arrested Development 시즌 3과 Dirk Gently’s Holistic Detective Agency도 비슷한 양상을 보인다.

바로전에 본 영화처럼 소동극 형태를 맡고 있다. 이 감독 영화들을 좀더 챙겨 봐야겠다.

별 2.5개 (재밌진 않지만 말리지는 않음)

뉴욕가서 사진을 많이 찍었는 데, 아직도 포커스나 명암 조절이 부족해서 그런지 제대로 쓸만한 사진이 많이 부족한거 같네요.

좀 더 익숙해져야될 것 같아용. 그래도 후보정을 잘 해두면 좀 살릴 수 있지 않을 까요? 좀 나중에 다시 한번 보고 살릴 수 있는 건 살려 봅시다.

그리고 필터도 새로 살래용

아이디란 인터넷 사이트에서 단순히 로그인을 위해 사용하는 identification이지만 대부분의 사람들은 모든 사이트에서 아이디를 동일하게 사용한다. 그래서 누군가의 아이디를 알게 된다면 그 사람이 인터넷에 올렸던 수 많은 글들을 확인하고 그 사람의 사고방식이나 생활 습관을 쉽게 알아낼 수 있다.

요즘들어서 SNS 때문에 인터넷으로 얼마나 쉽게 사람을 추적할 수 있는 지에 대해서 말이 많지만 사실 아이디로 추적하는 거는 내가 중학교 때였던 8년 전에도 충분히 가능했다. 옆 짝꿍이 초등학생 때 작성했던 인터넷 소설도 발견하고, 고등학교 때 친구가 사실은 거대한 커뮤니티의 네임드 였다는 것도 발견할 수 있었다.

우리나라 사람들이 가장 많이 사용하는 사이트는 단연컨데 네이버이다. 그 어떤 커뮤니티보다도 예전 부터 재미 있었던 건 네이버 뉴스 댓글창이다.

이제와서 예전 네이버 댓글을 찾기 힘들어서 그런지 이런 것 밖에 나오진 않지만 예전에는 이랬다. 글쓴이의 아이디도 번부 나오고 예전 글 보기를 통해서 재치있는 사람들의 댓글들을 많이 확인 할 수 있었다.

다만 문제점은 아이디라는게 이제는 개인 정보로 직접 연결이 되다 보니까 개인정보 보호를 위해 이제는 아이디의 일부만 보여주는 것으로 바뀌게 되었다. 위에 보면 알 수 있듯이 사실 이때는 IP주소마저 공개로 표시됐다.

그리고 이게 현재 모습이다. 각각 네이버 뉴스, 웹툰, 포스트다. 전부 아이디를 가려서 신상 보호에 도움을 준다. 즉 아무리 댓글로 자기가 백만장자라고 떠들어도 아이디를 검색해 사실은 거지였다~라는 건 밝힐 수 가 없는 것이다. 아마 이런 목적으로 네이버는 아이디를 가린 것 같다.

문제는 포스트다. 네이버 포스트는 약간 블로그 같은 느낌으로 사람들이 직접 글을 올릴 수 가 있다. 그리고 아이디 대신 닉네임을 사용 할 수 도 있는데, 많은 사람들은 포스트에 글도 올리지 않고 그냥 나두고 있다. 문제는 네이버 포스트의 기본 닉네임은 아이디고, 댓글의 아이디 부분만 클릭하면 바로 그 사람의 포스트를 들어 갈 수가 있다는 것이다.

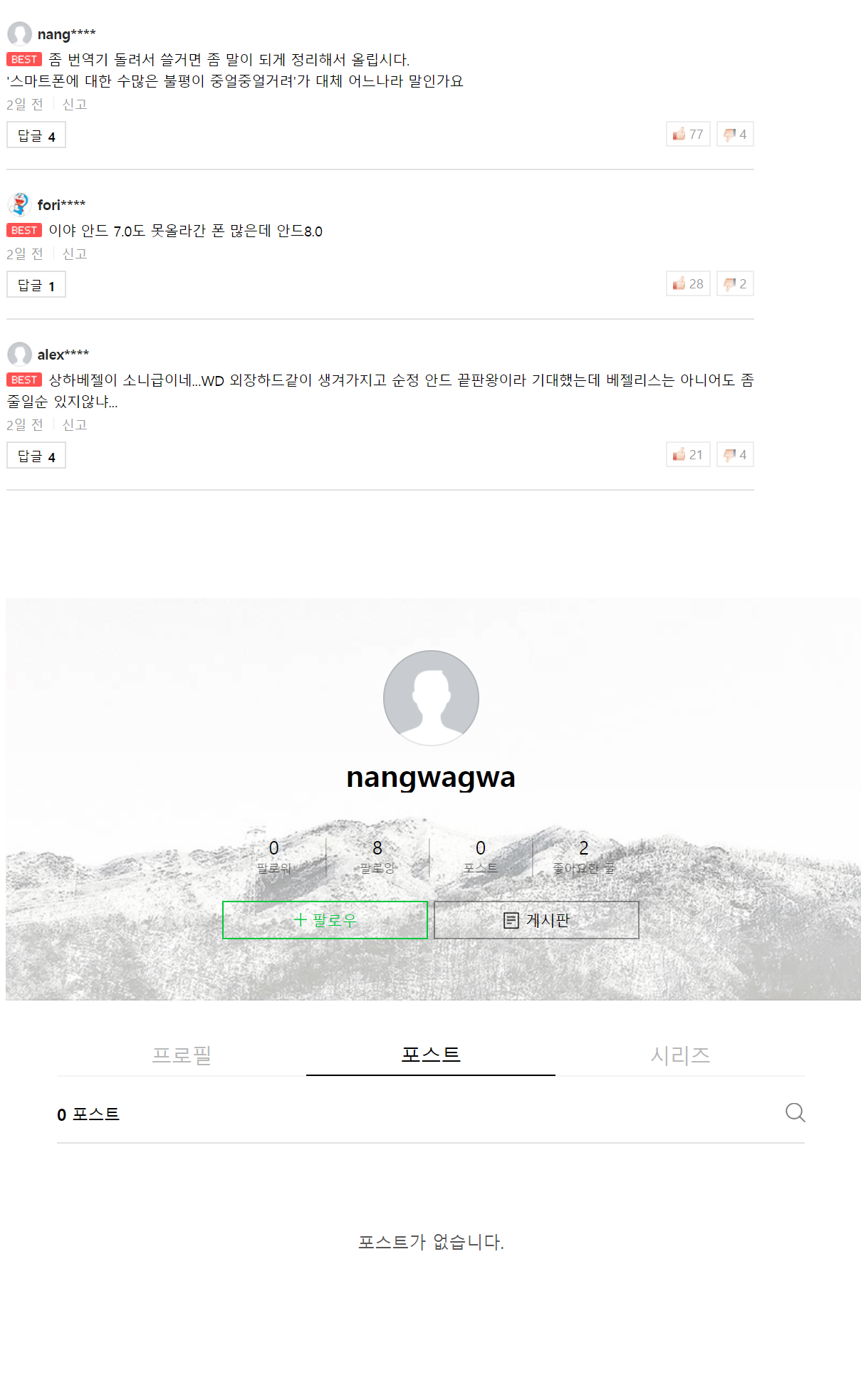보다 싶이 만약 내가 첫번째 댓글의 닉네임을 누른다면 그사람의 포스트로 들어가지며 그사람의 아이디는 그대로 노출 된다. 이 아이디를 내가 인스타그램에 검색한다던지해서 개인 정보까지 파악을 할 수 있다.

물론 아이디를 가리는 것은 의무가 아니다. 하지만 이왕가릴거면 제대로 가리자 네이버야.

[su_quote]The barber is the “one who shaves all those, and those only, who do not shave themselves.” The question is, does the barber shave himself?[/su_quote]

이발사의 역설은 누구나 한번 쯤은 들어본 유명한 역설입니다. 수학자 러셀이 누군가한테서 들었다고 자신에 책에 처음 적었다고 하네요. 워낙 유명해서 왠만한 사람들은 다 한번 씩 들어보았고 초등학교 수학관련 만화책에서도 왠만하면 나옵니다. 저는 메이플스토리 논리문제 만화책에서 처음 본 것 같네요.

한 마을의 이발사는 자신의 머리를 자르지 않는 모든 사람의 머리만 잘라줄 때, 이발사는 자기 자신의 머리를 자를 수 있을까, 라는 내용이 이발사의 역설입니다.

만약 이발사가 자신의 머리를 자른다고 생각해 봅시다. 그럼 이발사는 자신의 머리를 자르는 사람이기 때문에 자신의 머리를 잘라주면 안돼겠네요. 만약 자신의 머리를 자르지 않는다면 이발사는 자신의 머리를 자르지 않는 사람이니까, 자신의 머리를 잘라야 겠네요.

어느 선택을 해도 모순에 도달하는 ‘이 명제는 거짓이다’와 같은 역설처럼 보입니다.

오늘 계산이론 (Theory of Computation)이라는 수업을 들었는 데, 교수님이 이 역설을 대각선 논법으로 설명 해주신것이 인상 깊어서 이 글을 써봅니다. 대각선 논법은 실수가 비가산 집합임을 보여주는데도 사용하지만 이 글에서는 그정도 까지는 가지 않을 것 같네요. 그럼 대각선 논법을 간단히 설명해드리도록 하겠습니다.

O	X	O	O	O
X	O	X	X	O
X	O	X	X	O
O	X	O	O	X
O	O	X	X	X

다음과 같은 5X5 테이블을 있다고 할때 가로열을 각각

[latex]R_1 = \{1,3,4,5\} [/latex]

[latex]R_2 = \{2,5\} [/latex]

[latex]R_3 = \{2,5\} [/latex]

[latex]R_4 = \{1,3,4\} [/latex]

[latex]R_5 = \{1,2\} [/latex]

라고 봅시다. 즉 [latex] R_1 [/latex]는 첫번째 가로열에서 동그라미의 위치를 표현하는 집합입니다.

이제 이 테이블에서 대각선만 보면 순서대로 [latex] \{1,2,4\} [/latex] 가 됩니다 이것을 반전 시킨 것을 [latex] D = \{3,5\} [/latex] 라고 볼 때, 대각선 논법이란 것은 그 어느 가로열도 이것과 동일하지 않다는 것입니다. 즉 [latex] R_1, R_2, R_3, R_4, R_4 [/latex] 그 어느 것을 보아도 D와 동일하지 않다는 것을 확인 할 수 있습니다. 즉 이는

[latex] R_a \neq   D \forall a \in \{1,2,3,4,5\} [/latex]

로 볼 수 있고 이는 모든 가능한 [latex] N \times N [/latex]에 적용됩니다.

 

이제 다시 이발사 문제로 되돌아가 봅시다. 한번 이렇게 생각해 봅시다. [latex] R_a [/latex]란 a라는 사람이 머리를 잘라줄 수 있는 사람들의 집합으로 본다면, 1번 주민은 자기자신과, 3번, 4번, 5번 사람의 머리를 잘라줄 수 있겠네요.

어떤 마을 이라도 마을사람 수 x 마을 사람 수의 크기의 테이블을 만들 수 있고 이런 머리잘라주는 관계를 표현할 수 있습니다.

그렇다면 자기자신의 머리를 자를 수 없는 사람들의 집합은 D가 됩니다. D는 대각선의 반전이고 대각선에 동그라미가 표시된 사람들은 자기자신의 머리를 자를 수 있는 사람이기 때문입니다.

이발사가 머리를 잘라 줄 수 있는 사람은 [latex] R_{barber} [/latex]가 되겠고, 이발사가 마을 안에 있는 이상 이발사 역시 저 테이블 안에 들어있을 테니 대각선 논법에 의해 [latex] R_{barber} \neq D [/latex]가 될 수 밖에 없습니다.

즉 자기 자신의 머리를 자를 수 없는 사람만 잘라주는 이발사는 존재할 수 없는 것입니다.

 

1. TCG에서 상위호환이란 하나의 카드가 모든 면에서 다른 카드보다 우월할 때 쓰는 용어이다. 어느 하나가 모든 면에서 다른 것보다 우월하면 열등한 것은 도태 되는 것이 당연하다.

1. 예를 들어서 SSD는 처음 나왔을 때 HDD보다 월등하게 빨랐지만, 가격면에서 더 안 좋았기 때문에 현재 SSD와 HDD는 서로 공존하는 상태이다. 만약 SSD가 속도, 물리적 크기, 가격면에서 전부 더 나았다면 HDD는 빠르게 도태되어 사라졌을 것이다. 하지만 서로 서로 장단점이 있기 때문에 SSD는 HDD의 상위호환이라고 부르기는 힘들다.

2. 이렇듯 한 제품이 다른 제품보다 모든 면에서 가격을 포함한 모든 면에서 낫다면 열등한 제품은 존재의 의미가 없으며 사라져야한다.

1. 어린이용 치약은 일반 치약의 상위호환이다. 어린이용 치약과 일반 치약의 성능은 똑같다. 불소가 포함되어 있다면 어린이용 치약은 일반 치약과 성능면에서 전혀 차이가 없다. 가격 면에서도 동일하다. 가장 큰 차이는 어린이용 치약은 일반 치약처럼 자극적이지 않고 (어린이들은 맵다고 표현한다), 기분좋은 딸기맛과 향이 나는 것이다.

2. 이렇듯 어린이용 치약은 일반 치약에 비교해서 더 나쁜 점이 없는 상위호환이기 때문에 일반 치약이 아닌 어린이 용 치약이 더 낫다. 가끔씩 일반 치약은 입이 시원한 맛이 난다고 하는데 그런 새끼들은 딸기맛 아이스크림이 아니라 시원한 치약맛 아이스크림을 먹는가 보다.

3. 같은 이유로 눈에 들어가도 아프지 않은 어린이용 샴푸는 일반 샴푸의 상위 호환이다.

한번도 눈치를 못채다가 얼마전에 알게 된 사실이 있는데 바로 내 타자 습관에서 오른 손이 독수리 타인걸 알게 되었다. 사실 키보드를 안보고 치기 때문에 별로 생각을 안했는데 보니 오른쪽은 거의 전부 검지로 해결을 한다. 이 정도만 해도 사실 400타는 나오지만 문제는 버튼의 위치를 손목의 감으로 찾기 때문에 키보드가 바뀌면 오타량이 엄청나게 늘어난다. 영타도 어깨에 힘주고 집중해야지 겨우 300타가 되는 수준이다. 그나마 한글은 자음 모음이 따로 배열되어 있어서 자음을 치는 동안 오른손 검지 손가람이 모음을 찾아갈 시간이 있지만, 영어의 경우 오른손을 연속으로 쓰는 경우도 많기 때문에 약간 속도가 더딘다.

많이 늦었지만 습관을 다시 고쳐 잡아서 영한 둘다 500타를 넘겨보도록 하자.